Területszámítással kapcsolatos feladat, 7. osztály

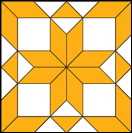
Egy 20 cm oldalú négyzet alakú mintát egyenlő szárú derékszögű háromszög, négyzet, illetve paralelogramma alakú csempékkel raktunk ki. Mekkora egy paralelogramma alakú csempe területe?

1. Tudjuk, hogy a négyzet a függőlegesen és vízszintesen is szimmetrikus, sőt, a csempéket is ezek figyelembe vételével helyeztük el. Ha a négyzetet ezen szimmetria-tengelyek mentén elvágjuk, négy egyenlő nagyságú négyzetet kapunk, melyek mindegyikében ugyanannyi és ugyanolyan csempék láthatók (vagyis a négy rész egymással egybevágó.)

2. Vizsgáljunk meg egy negyed csempét! Láthatjuk, hogy a fehér, négyzet alakú csempe egy oldalának hossza megegyezik a sárga paralelogramma alakú csempe hosszabb oldalának hosszával, illetve egy paralelogramma alakú csempe kirakható két egyenlő szárú derékszögű háromszögből.

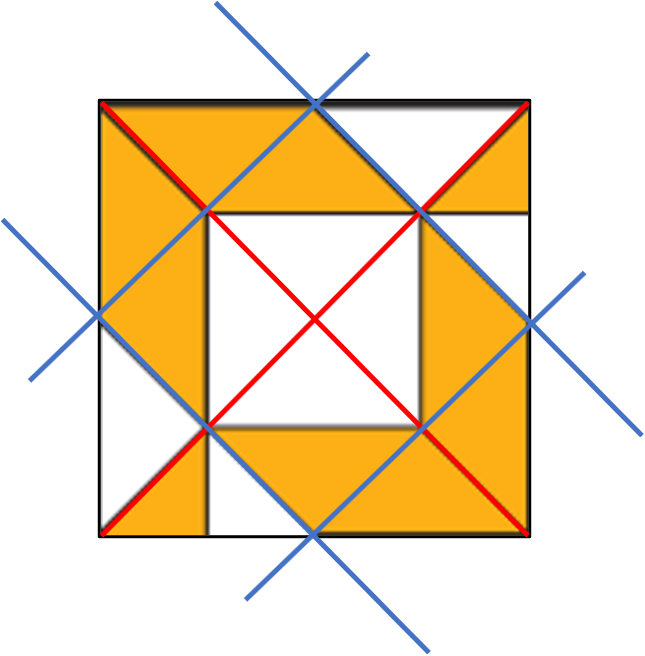
3. Az előzőek alapján láthatjuk, hogy az eredeti ábra ¼ része kirakható 16 db egybevágó egyenlő szárú derékszögű háromszögből. Az ábráról az is leolvasható, hogy a háromszögek alapja 5-5 cm, mely hosszúság megegyezik a paralelogramma hosszabb oldalának hosszával. Azt is látjuk, hogy a kékkel jelölt háromszög ugyancsak felosztható két egybevágó egyenlő szárú háromszögre, melynek oldalhossza 2,5 cm. A kis háromszög oldalhossza adja meg a sárga paralelogrammák magasságát is.

4. Egy paralelogramma alakú csempe területe tehát az alap és a hozzá tartozó magasság szorzata, azaz T = 5 × 2,5 = 12,5 cm²